ExcelとPythonのソルバーを使っての線形最適化問題演習ー1
並木誠著『Pythonによる数理最適化入門』(朝倉書店)に載っている最初の問題を参考に、
ExcelとPythonのソルバーを使って問題を解いてみる。
(問題)
製品A、製品B、製品C という製品が3つある
原料a、原料b、原料c という原料が3つある
製品A を1つ生産するのに、原料aを3kg、原料bを1kg 必要とする
製品B を1つ生産するのに、原料aを1kg、原料bを3kg、原料cを2kg 必要とする
製品C を1つ生産するのに、原料aを2kg、 原料cを4kg 必要とする
原料の在庫量は、原料a が60kg、原料b が36kg、原料c が48kg である
製品1個ごとの販売利益は、製品A が150円、製品B が200円、製品C が300円である
販売利益を最大にするには、それぞれ何個づつ生産すればよいか?
またその金額はいくらになるか?
まず、Excel のソルバーで解く
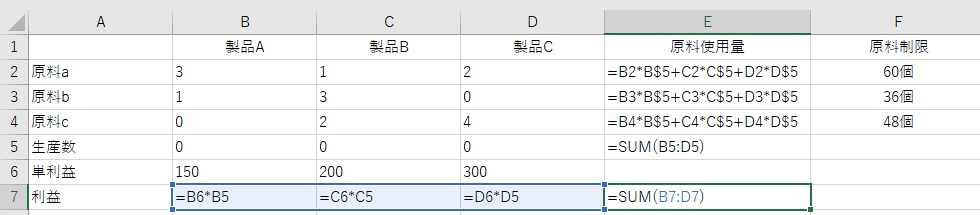
問題を表にまとめると以下のようになる

各セルに設定された式を表示
ソルバーを使えるようにする。(「ファイル」-「オプション」-「アドオン」-「ソルバーアドオン」をアクティブにする)
「データ」-「ソルバー」をクリックして、下記のように設定する
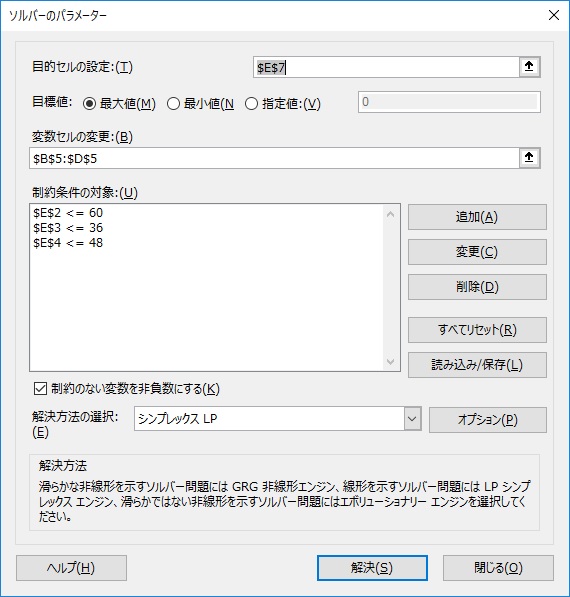
上記のように設定後、「解決」をクリックする
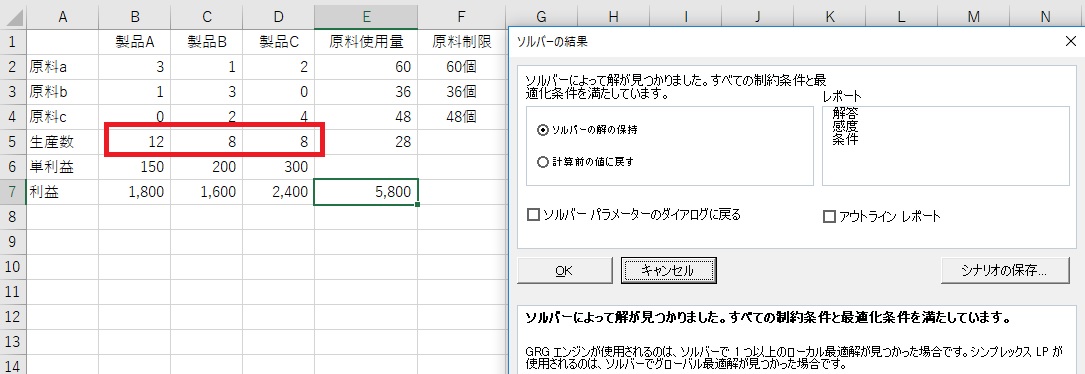
(解)
製品A 12個、 製品B 8個、 製品C 8個 の生産で、最大利益は 5,800円となる
次に、Python のソルバーで解を求める
ソルバーを使えるモジュール Pulp をインポートする(まだのときは、pip install pulp でインストールする)
jupyter notebook 上で作成する
# Python上で数理最適化問題を簡単にコーディングできるモデリングAPI、モデリング言語 pulp をインポート
import pulp
lp = pulp.LpProblem('lp-test', pulp.LpMaximize)
# 求める生産数の設定(製品Aの生産数 xA,、製品Bの生産数 xB、製品Cの生産数 xC)
# xA >= 0, xB >= 0, xC >= 0
xA = pulp.LpVariable('xA', 0)
xB = pulp.LpVariable('xB', 0)
xC = pulp.LpVariable('xC', 0)
# 評価関数の設定
lp += 150 * xA + 200 * xB + 300 *xC
# 制約条件の設定
lp += 3 * xA + xB + 2 * xC <= 60
lp += xA + 3 * xB <= 36
lp += 2 * xB + 4 * xC <= 48
# 最適化問題の確認
print(lp)
# 求解
lp.solve()
# 結果
print('製品Aの生産個数:%d 個' % xA.value())
print('製品Bの生産個数:%d 個' % xB.value())
print('製品Cの生産個数:%d 個' % xC.value())
print('')
print('最大利益:{:,.0f} 円'.format(150 * xA.value() + 200 * xB.value() + 300 * xC.value()))
「Shift」+「Enter」で実行すると
lp-test:
MAXIMIZE
150*xA + 200*xB + 300*xC + 0
SUBJECT TO
_C1: 3 xA + xB + 2 xC <= 60
_C2: xA + 3 xB <= 36
_C3: 2 xB + 4 xC <= 48
VARIABLES
xA Continuous
xB Continuous
xC Continuous
製品Aの生産個数:12 個
製品Bの生産個数:8 個
製品Cの生産個数:8 個
最大利益:5,800 円
となり、Excelのソルバーと同じ結果を得る