ExcelとPythonのソルバーを使っての線形最適化問題演習ー４　情報処理試験２種問題

『平成１０年秋　情報処理試験2種』の問題を参考に、
ExcelとPythonのソルバーを使って問題を解いてみる。

（問題）
ある工場で製品A、Bを生産している。

製品Ａを1トン製造するのに、原料P,Qをそれぞれ４トン、９トン必要とし、
　製品Ｂについてもそれぞれ８トン、６トン必要とする。

　 また、製品Ａ，Ｂは1トンあたり2万円、3万円の利益を生む。
　しかし、原料はPは４０トン、Qは５４トンしかない。

　利益を最大にする製品Ａ，Ｂの生産量をソルバーを使用して求めなさい。

まず、Excel のソルバーで解く
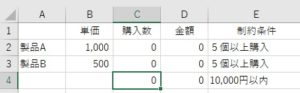
問題を表にまとめると以下のようになる


各セルに設定された式を表示


ソルバーを使えるようにする。（「ファイル」－「オプション」－「アドオン」－「ソルバーアドオン」をアクティブにする）
「データ」－「ソルバー」をクリックして、下記のように設定する


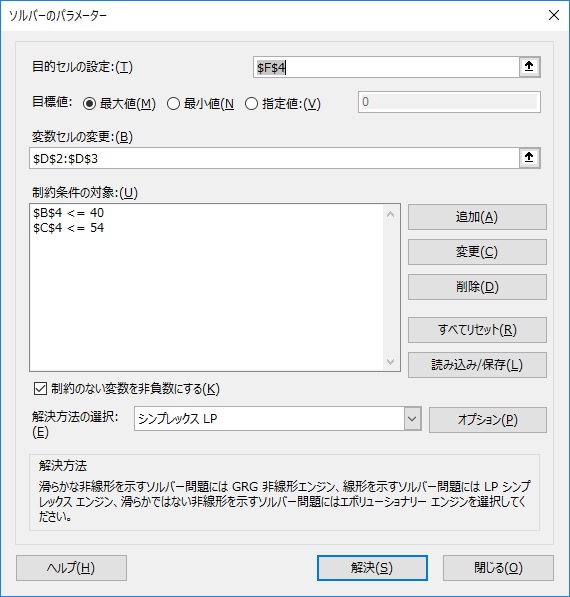
上記のように設定後、「解決」をクリックする


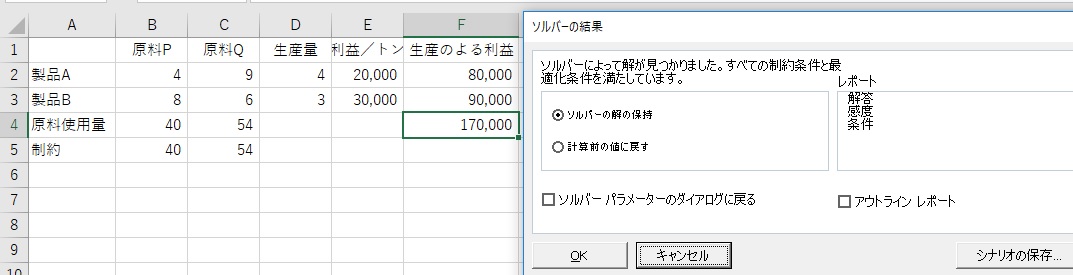
（解）
　　　製品A　を　４トン、　製品B　を　３トン　生産すると、最大利益が　１７０，０００　円　となる

次に、Python のソルバーで解を求める
ソルバーを使えるモジュール Pulp をインポートする（まだのときは、pip install pulp でインストールする）
jupyter notebook 上で作成する

# Python上で数理最適化問題を簡単にコーディングできるモデリングAPI、モデリング言語 pulp をインポート
import pulp

lp = pulp.LpProblem('lp-test4', pulp.LpMaximize)

#  求める生産数の設定(製品Aの生産量 xA,、製品Bの生産量 xB)

#      xA >= 0, xB >= 0
xA = pulp.LpVariable('xA', 0)
xB = pulp.LpVariable('xB', 0)

#   評価関数の設定
lp += 20000 * xA + 30000 * xB

#   制約条件の設定
lp += 4 * xA + 8 *xB  <= 40
lp += 9 * xA + 6 * xB <= 54

#   最適化問題の確認
print(lp)

#   求解
lp.solve()

#   結果
print('製品Aの生産量：%d トン' % xA.value())
print('製品Bの生産量：%d トン' % xB.value())
print('')
print('最大利益：{:,.0f} 円'.format(20000 * xA.value() + 30000 * xB.value()))

「Shift」＋「Enter」で実行すると

lp-test4:
MAXIMIZE
20000*xA + 30000*xB + 0
SUBJECT TO
_C1: 4 xA + 8 xB <= 40

_C2: 9 xA + 6 xB <= 54

VARIABLES
xA Continuous
xB Continuous

製品Aの生産量：4 トン
製品Bの生産量：3 トン

最大利益：170,000 円

となり、Excelのソルバーと同じ結果を得る