3つの直角三角形を求めるーWOWOWつるさんかめさん和算第一回目への代数的解法
WOWOWのつるさんかめさんの和算第一回目の問題:
長方形に内接する3つの直角三角形があり、
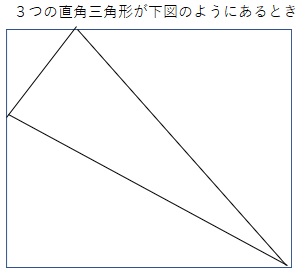
そのすべての辺の長さが整数になる場合を求めよ。
この図を下図のように
①②③の3つの直角三角形とする
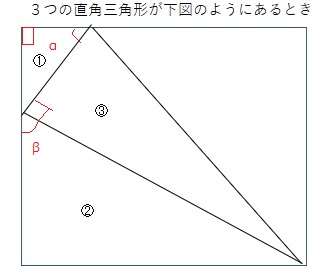
直角三角形①②で
①の外角 90 + α
②の内角 β + 90
が同じなので 90 + α = β + 90
α = β となり
「直角以外の角度の1つが等しい」ので
直角三角形①② は相似である。
以上を元に、代数的なアプローチで解法を試みる。
①②③の3つの直角三角形があり
以下の4つの条件:
1.3つの直角三角形の辺の長さは整数である
2.①と②の直角三角形は相似である
3.①の「斜辺」と③の「高さ」が同じ長さ
4.②の「斜辺」と③の「底辺」が同じ長さ
以上の4つの条件を満たす3つの直角三角形を求める。
1の条件より
3辺が整数となる直角三角形の3辺の長さの比をとり、共通数で割っていくと、基本となる整数比が求められる。
2の条件より
①と②の 高さ:底辺:斜辺 の基本の整数比を a:b:c (a,b,cは整数)とする。
③の 高さ:底辺:斜辺 の基本の整数比を e:f:g (e,f,g は整数)とする。
3、4の条件より
①は基本比率の x倍(x は整数)とすると、3辺の長さは 高さ=ax, 底辺=bx, 斜辺=cx となる。
②は基本比率の y倍(y は整数)とすると、3辺の長さは 高さ=ay, 底辺=by, 斜辺=cy となる。
③は基本比率の z倍(z は整数)とすると、 3辺の長さは 高さ=ez, 底辺=fz, 斜辺=gz となる。
条件3より、cx = ez
条件4より、cy = fz
この連立方程式を解くと
(fz/y)x = ez
fx = ey
x = (e/f)y
x, e, f, y ともに整数であり、また、直角二等辺三角形の斜辺は整数でないため、e と f は同じ値ではない。
x が整数になるには、 y は f の倍数
同様に y = (f/e)x となり、
y が整数になるには、 x は e の倍数
3辺の長さである 高さ、底辺、斜辺 の基本の整数比を (a, b ,c)と書き表わすと、
3つの辺の基本比率の例として (3, 4, 5)や(5, 12, 13) がある。
例として
①と②の3辺の基本比率(a, b, c)を (3, 4, 5) とし、
x, y の e, f の倍率を 1 としたとき、x = e, y = f となり
z は z = (x/e)c のため z = c となる。
以上より
①の3辺の長さは e x (3, 4, 5) = 3e, 4e, 5e
②の3辺の長さは f x (3, 4, 5) = 3f, 4f, 5f
③の3辺の長さは 5 x (e, f, g) = 5e, 5f, 5g
Ⅰ③の3辺の基本比率(e, f, g)を(3, 4, 5)としたとき
①の3辺の長さは、 9, 12, 15
②の3辺の長さは、 12, 16, 20
③の3辺の長さは、 15, 20, 25
Ⅱ③の3辺の基本比率(e, f, g)を(5, 12, 13)としたとき
①の3辺の長さは、 15, 20, 25
②の3辺の長さは、 36, 48, 60
③の3辺の長さは、 25, 60, 65
①と②の3辺の基本比率(a, b, c)を (5, 12, 13) とし、
x, y の e, f の倍率を 1 としたとき、x = e, y = f , z =c となり
①の3辺の長さは e x (5, 12, 13) = 5e, 12e, 13e
②の3辺の長さは f x (5, 12, 13) = 5f, 12f, 13f
③の3辺の長さは 13 x (e, f, g) = 13e, 13f, 13g
Ⅲ③の3辺の基本比率(e, f, g)を(3, 4, 5)としたとき
①の3辺の長さは、15, 36, 39
②の3辺の長さは、 20, 48, 52
③の3辺の長さは、 39, 52, 65
Ⅳ③の3辺の基本比率(e, f, g)を(5, 12, 13)としたとき
①の3辺の長さは、 25, 60, 65
②の3辺の長さは、 60, 144, 156
③の3辺の長さは、 65, 156, 169
以上、
$$_1 P_1 = 1 $$ 基本比率を1個使うと、Ⅰのみの1パターン
基本比率を2個使うと、Ⅰ~Ⅳの4パターン
Ⅰの3つの直角三角形を和算の図のように並べてみよう。
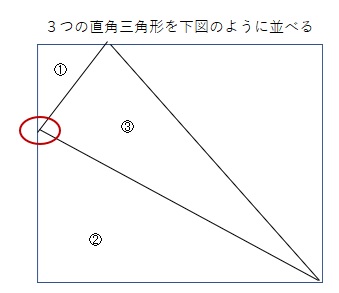
①と②は相似のため、赤の〇内は角度の和が180度となり一直線となる。
外枠の長方形の辺は、直角三角形の整数の辺からなるため、これも整数となる。
Ⅱ~Ⅳも同様である。
以上により、
この4組の3つの直角三角形は
WOWOWのつるさんかめさんの和算第一回目の答え に該当する。
これは、対象のなかから1個、または2個選択する場合の数を算出する順列組み合わせであり、選択の順番も意味をもつことにより
「順列」の式が当てはまる。
3つの辺の基本比率を1つ使用したとき
できるパターン数は\begin{eqnarray*}_1 P_1 = 1 \end{eqnarray*} 3つの辺の基本比率を2つ使用したとき
できるパターン数は\begin{eqnarray*}_2 P_1 + _2 P_2 = 2 + 2 = 4 \end{eqnarray*} 3つの辺の基本比率を3つ使用したとき
できるパターン数は\begin{eqnarray*}_3 P_1 + _3 P_2 = 3 + 3*2 = 9 \end{eqnarray*} 3つの辺の基本比率をn個使用したとき
できるパターン数は\begin{eqnarray*}_n P_1 + _n P_2 = n + n(n-1) = n^2 \end{eqnarray*}
まとめると、
WOWOWのつるさんかめさんの和算第一回目は
使用する基本比率の数に応じて
その数の2乗の答え(パターン)が存在する。
以上をもって、解法完了。
【補足】
直角三角形の3平方の定理で、3つの辺が自然数のときにその3つの組み合わせをピタグラス数という。3つの数が互いに公約数を持たない素のときを特に、原子ピタゴラス数という。ピタグラス数を持つすべての直角三角形は、原始ピタゴラス数を持つ直角三角形を整数倍したものである。
上記の基本比率は、原始ピタゴラス数のことである。
原始ピタゴラス数は、a が10以下でも
( 3, 4, 5 )、( 5, 12, 13 )、( 7, 24, 25 )、( 8, 15, 17 )、( 9, 40, 41 )というように、5個存在する。
この5個を利用すると、52 で 25個のパターンを得る
自然数全体を見ると、その数は無数に存在する。