公園を巡回する周遊ルートをソルバーを使って求める
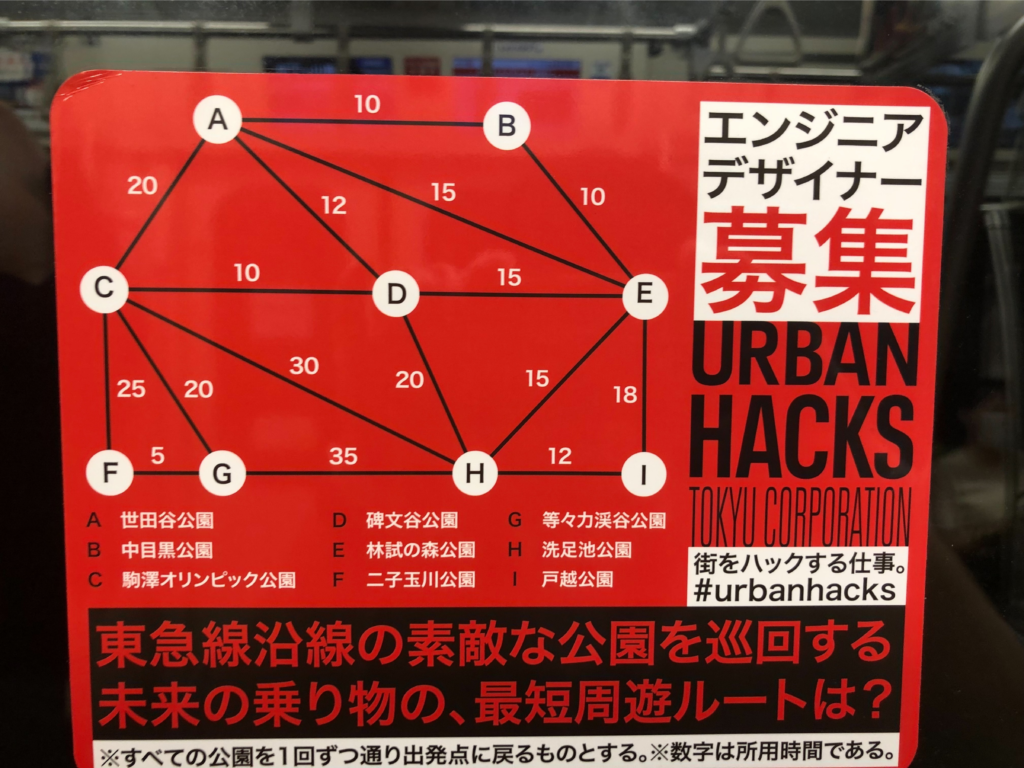
これは、「巡回サラリーマン問題」という命題で有名で
この問題の解答をExcelのソルバーで試みる。
Excelのシートに以下のようにものを作成する。
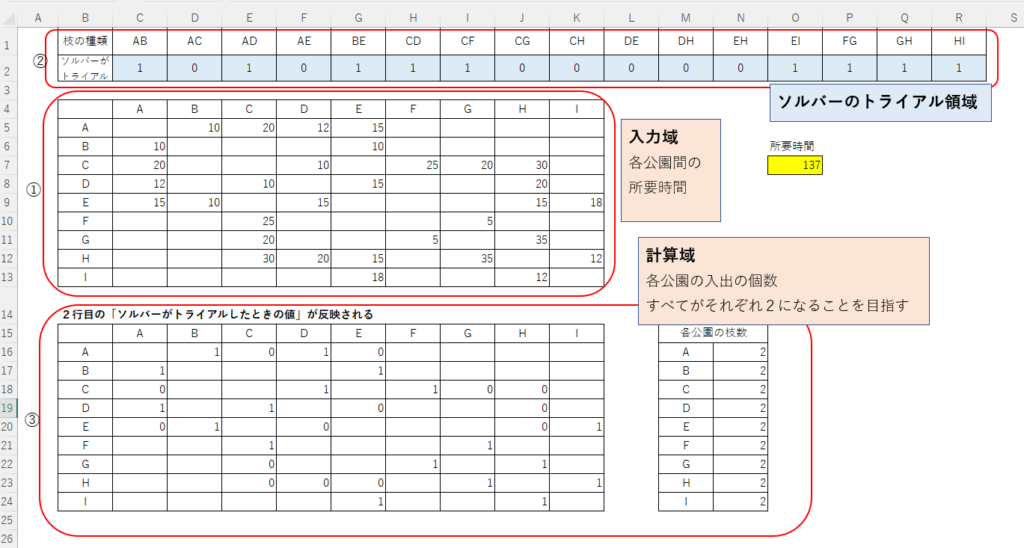
①で各公園間の所要時間を入力する。
②各公園間でつながっている線(グラフ理論では、これをエッジ(枝)という)をすべて挙げる。
2行目は、ソルバーが1(通る)または0(通らない)を設定するので、未入力でOK
③ソルバーがトライアルしたときの値を反映する。
上図でいえば、
セルD16とC17 に 式 =C2、セルE16とC18 に 式 =D2、
セルF16とC19に 式 =E2、セルG16とC20に 式 =F2、...
...セルK23とJ24に 式 =R2 を設定する
右の「各公園の枝数」欄には、 各公園ごとの枝数の合計値を設定する
セルN16には 式 =sum(C16:K16)
セルN17には 式 =sum(C17:K17)
...
この合計値がすべて2となるとき、
すべての公園は入出の2本で1回しか通らないことになる。
背景色が黄色の合計の所要時間セルO7には
式 =D5*D16+E5*E16+F5*F16+G5*G16+G6*G17+F7*F18+H7*H18+I7*I18+J7*J18
+G8*G19+J8*J19+J9*J20+K9*K20+I10*I21+J11*J22+K12*K23
を設定する。
「データ」ー「ソルバー」を選択し、以下のようにパラメータを設定する。
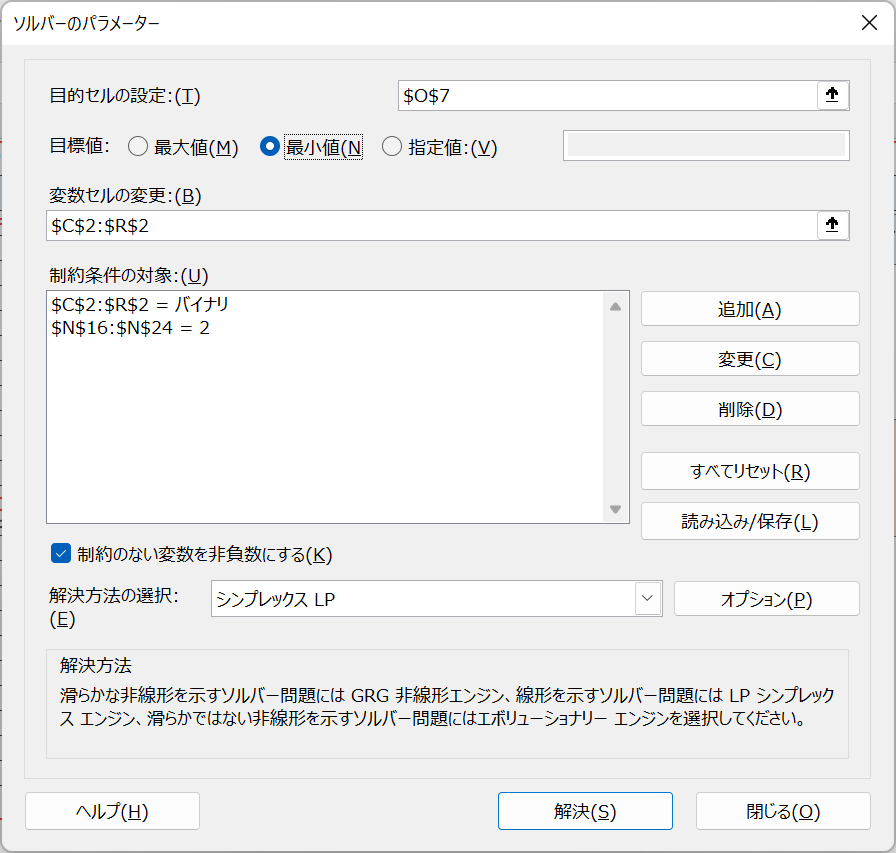
「解決」ボタンをクリックする。
以下のような解が得られる。

線がつながるのは、AB、AD、BE、CF、CG、DH、EI、FG、HI となる。
これをつないでいくと、
AB→BE→EI→IH→HD→DA、CF→FG→GC となり、
2つに分断され、すべての公園が線でつながらない。
ソルバーの目標値を 「最大値」 に変更して再度試みる。
すると以下のような解が得られる。

線がつながるのは、AB、AD、BE、CD、CF、EI、FG、GH、HI となり
これをつないでいくと
AB→BE→EI→IH→HG→GF→FC→CD→DA となり
すべての公園が線でつながる。
所要時間の最小値(132分)と最大値(137分)の間に解があるかどうかを調べる。
ソルバーの目標値に指定値を選択し、133~136までの数を1つづつ入力して解を求める。
すると、133~136までの間で指定値を満たす解は1つも存在しない。
よって、
各公園を一回ずつ通り出発点に戻ってくる巡回ルートは、
1つしかなく、その所要時間は137分である。
以上。
